p-value
The p-value is a number between 0 and 1 that indicates how surprising a study's results would be if there was actually no effect, as long as the study and statistical analyses are well-designed.
Last Updated:July 17, 2023
Summary
Introduction: The purpose of the p-value
Science is all about testing hypotheses. You start with some idea about how some aspect of the world works, then you collect data to test your idea.
The starting hypothesis that an intervention (a diet, for instance, or a supplement) will make no difference, when compared to a placebo or some other control, is called a null hypothesis. Null hypotheses are the most common type of hypothesis scientists put to the test.
Let’s say you test creatine against a placebo. The null hypothesis isn’t that creatine will increase strength more than the placebo will, but that it won’t. If your experiment nevertheless shows that creatine outperforms the placebo (or vice versa), this positive result goes against your null hypothesis, and so you are “surprised”.
Couldn’t the positive result you found be due to chance, though? How unlikely would that be? In other words, how surprised should the positive result make you, if you assume chance alone is what’s at play? As surprised as if you got heads twice in a row on a coin toss? Or as surprised as if you got heads forty times in a row?
To “quantify your surprise” at the positive result, you can determine a p-value for this result. The lower the p-value, the more surprising it would be to get this result by chance if the null hypothesis were true. In other words, the lower the p-value of a positive result, the less likely it is for this result to be due to chance, and thus for an effect to be a false positive.
When you run a study, you usually start with a null hypothesis. In other words, you start with the hypothesis that what you will test will make no difference. If you do find a difference anyway, you are “surprised”. The p-value is a measure of this surprise; the lower the p-value, the more strongly the result contradicts your null hypothesis.
The p-value ranges from 0 to 1. As the evidence gets more surprising, the p-value will get closer to 0. The more surprising the data (i.e., the bigger the difference from the result expected under the null hypothesis), or the more of that surprising data you’ve collected (for eg. the more people you’ve tested), the smaller the p-value will be. This makes sense if you think about it. If you assume an intervention makes no difference, then seeing a big difference means it’s more likely that your assumption is wrong; likewise for seeing a difference over and over and over. The closer the p-value is to 0, the more confident you can be in rejecting the null hypothesis.
The p-value ranges from 0 to 1. As the evidence gets more surprising assuming the null hypothesis, the p-value will get closer to 0. This can happen when more data are collected or bigger differences are observed. The lower the p-value, the more confident you can be in rejecting the null hypothesis.
Example: Coin flip experiment
As an example, imagine I have a coin, and I want to know whether it's a fair coin (equal chance of landing on heads or tails). My null hypothesis is that this coin is fair. If I flip that coin ten times and I get five heads, what's the p-value of the data I collected? Well, with a fair coin, I would expect to get at least five heads about 62 times out of 100. (See this calculator: https://www.omnicalculator.com/statistics/coin-flip-probability ) So p=0.62. However, if I flipped that coin ten times and I got zero heads, then the p-value of my data would be p=0.001: if I flipped a fair coin ten times, I would expect to get no heads only about one time in 1024 experiments.
The second experiment, when I flipped the coin ten times and got zero heads, had results that were very surprising assuming that the coin is fair. The fact that the data were so surprising provides me with strong reason to reject the null hypothesis (the hypothesis that my coin is fair), presuming my other assumptions hold (see the "Digging Deeper" box above). The first experiment, when I flipped ten times and I got five heads, yielded results that wouldn’t be surprising at all assuming the null hypothesis (of a fair coin) was true. So that experiment didn’t provide a good reason to reject the null hypothesis.
If I wanted to be even more sure, I could repeat the experiment, perhaps with more flips. If I get similarly surprising results, I have even more reason to think the coin is unfair and that I should reject the null hypothesis. This makes sense if you think about it. If you see a difference over and over again when you don’t expect one, the world around you is not behaving as you assume it does! Collecting a lot of data can also help bring out smaller effects. If I flip a different coin 10 times and get 6 heads, p=0.37 (the odds of getting at least six heads with ten flips of a fair coin). My experiment didn’t give me a good reason to reject the null hypothesis. But if I flip that coin 100 times and get 60 heads, p=0.03 (the odds of getting at least sixty heads with one hundred flips of a fair coin). Now my experiment is giving me a good reason to believe that the coin isn’t fair after all.
Application: Understanding the p-values you see in studies
These lessons can carry over to health and nutrition research. Looking at multiple studies examining the same topic can make you more confident in rejecting the null hypothesis. And studies with larger sample sizes (analogous to flipping a coin more times) can provide more confidence that an effect is real (as long as there’s nothing funky about the study design).
In summary, if the evidence gets too surprising, you have reason to believe that the null hypothesis is incorrect. If the p-value is really low, you can reject the null hypothesis. But how low is low enough? That’s an open question whose answer is somewhat arbitrary. Most papers use a cutoff of p=0.05: if a p-value is less than this, it’s called “statistically significant,” and if it’s above this, it’s not. However, statistical significance is the topic for another glossary entry. For our purposes here, just think of the p-value as a measure of how surprising the data are if you assume the null hypothesis is true. While strict cutoffs are often used in practice, they don’t have to be. And in some cases (especially exploratory research) it may be best to not use a cutoff at all!
If you found that all a bit hard to digest, you’re not alone. A lot of people find p-values unintuitive, and it’s not uncommon to struggle with them. To help out, there’s a visual summary of how surprising you should find the data (assuming the null hypothesis is true!) for some different p-values in Figure 1.
Figure 1: Just how surprising are different _p_-values, anyway?
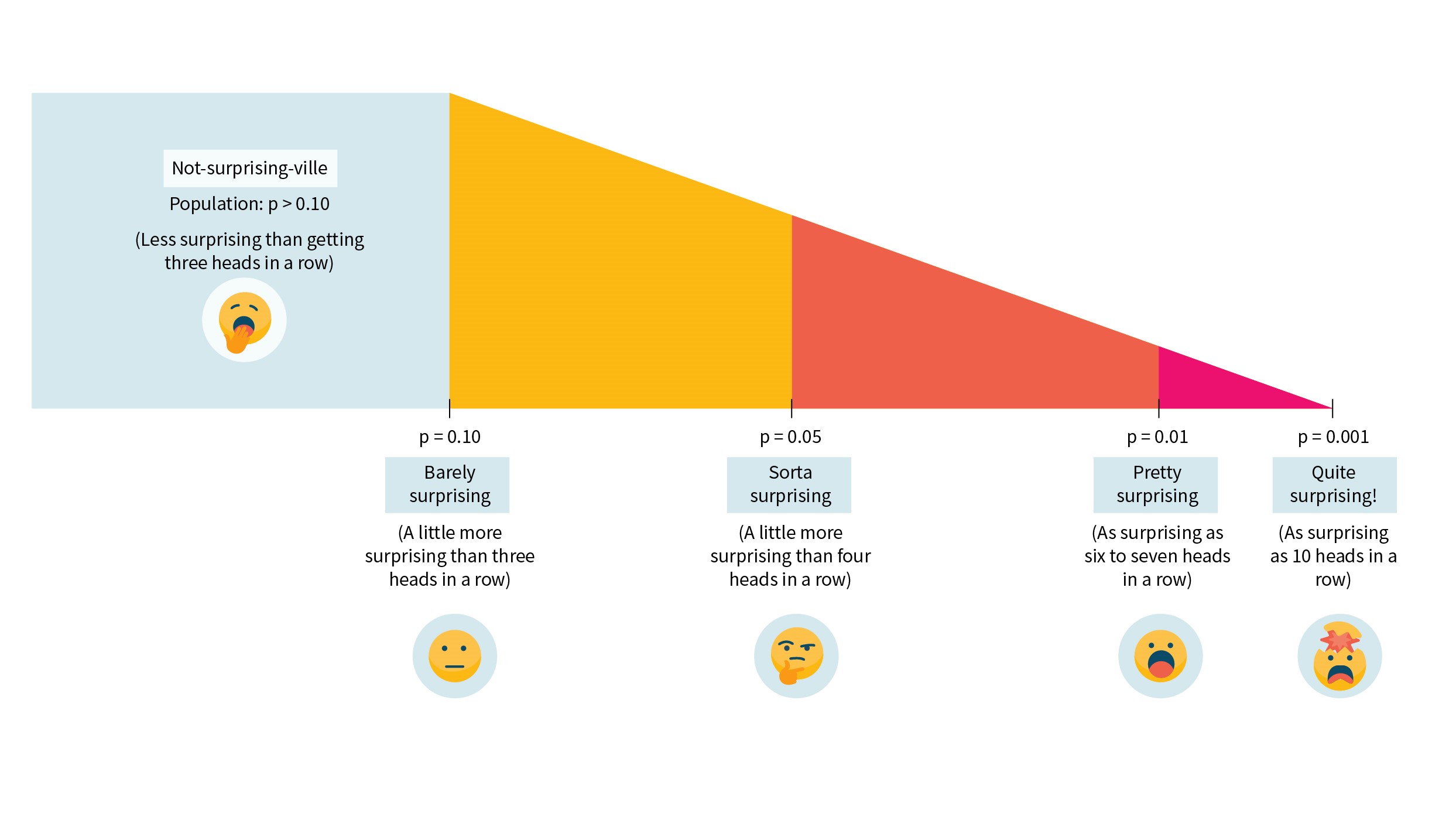
Reference: Rafi and Greenland. BMC Med Res Methodol. 2020 Sep. PMID: 32998683
If the data would be too surprising if the null hypothesis were true, it’s a reason to reject the null hypothesis. The usual cutoff for how surprising is “too surprising” is a p-value of less than 0.05. When the p-value is less than 0.05, the results are called “statistically significant”.